
Quem trabalha no “domínio” da biodiversidade tem a clara percepção de que ela é “transversal” a tudo. A manifestação da biodiversidade está presente nas questões sociais, saúde, cultura, direitos e cidadania, ciência, tecnologia, educação e economia, cobrindo todos os “eixos temáticos”.
Somado a esta característica – a transversalidade temática – aprendi com o professor Jorge Xavier da Silva, da UFRJ, pioneiro do geoprocessamento no Brasil, que dizia que “o fato biológico nunca está dissociado do fato ambiental“. A mais pura verdade! Obrigado professor!
Para complicar ainda mais, na camada mais interna desta “cebola de relações”, as espécies se relacionam entre si de formas e intensidades que mal conhecemos.
Como sabem, minha área profissional é a “Gestão de Informação sobre Biodiversidade” e esta complexidade de relações “multi-camada” não contribui em nada para minimizar meus transtornos de ansiedade! Pior. Até pouco tempo atrás, as ferramentas (no caso, “Sistemas Gerenciadores de Bancos de Dados” – SGBDs) que tínhamos eram extremamente limitadas para implementar um eventual modelo que descreva a complexidade destas relações.
Um dos primeiros cursos que fiz ligado a área de TI, no final dos anos 80, foi de “Modelagem de Bancos de Dados”. Mudou minha vida. Entendi os bancos de dados chamados de relacionais, fui apresentado a álgebra relacional, aprendi o “Modelo de Entidades e Relacionamentos” (Modelo E-R), e passei a desenhar bancos de dados usando papel e lápis. Desta capacitação surgiu meu primeiro sistema “sério”, publicado em 1991. Deste ponto em diante, meu relacionamento com bancos de dados relacionais foi crescendo e se consolidando. Aprendi SQL e gerenciar dados com SGBD era tudo de bom. Todo mundo conhecia, usava e respeitava. Porém, algo me incomodava.
Em 2000, lendo este artigo, percebi que meu desconforto com os SGBDs relacionais na lida com dados de biodiversidade era compartilhado por colegas da área. Em resumo, ficava claro a limitação dos SGBDs relacionais para representar a complexidade de questões taxonômicas. Se apenas nas “questões taxonômicas” bancos de dados relacionais já são limitados, imaginem implementar um banco de dados que consiga armazenar e recuperar a complexidade de todas estas “camadas de relações”, nesta transversalidade.
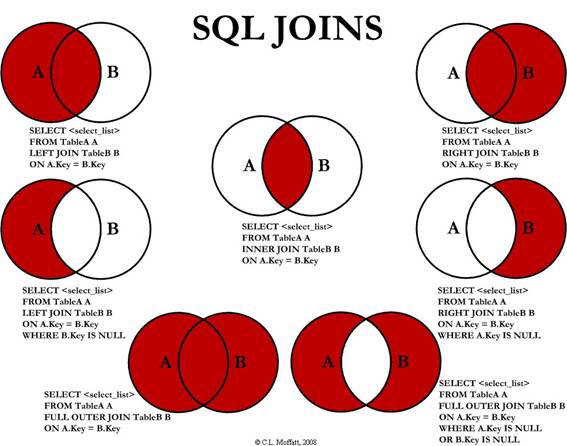 Sem querer ser muito técnico, que não é esse o foco aqui, relações são representadas (e recuperadas) em bancos de dados relacionais através de um “JOIN“. Além de não ser exatamente “simples”, possui um custo computacional altíssimo, há muito tempo conhecido e temido. Quanto mais “JOINs” na consulta, para representar relações, mais “lento” fica o sistema. Simples assim. Não vou sequer entrar na questão da “escalabilidade horizontal” de bancos de dados SQL, pois é outro fator limitante.
Sem querer ser muito técnico, que não é esse o foco aqui, relações são representadas (e recuperadas) em bancos de dados relacionais através de um “JOIN“. Além de não ser exatamente “simples”, possui um custo computacional altíssimo, há muito tempo conhecido e temido. Quanto mais “JOINs” na consulta, para representar relações, mais “lento” fica o sistema. Simples assim. Não vou sequer entrar na questão da “escalabilidade horizontal” de bancos de dados SQL, pois é outro fator limitante.
 Pois bem, tudo isso ai em cima é para chegar neste ponto onde quero declarar explicitamente minha nova “paixão” (deixando claro para minha doce Claudia, “paixão profissional!”). Depois de muito adiar, aproveitando essa pandemia, dediquei parte do meu tempo a estudar os bancos de dados orientados a grafos na desconfiança de que eles seriam uma abordagem interessante para lidar com esta complexidade de relações da biodiversidade, em suas diferentes camadas. Cada vez mais, me convenço disto.
Pois bem, tudo isso ai em cima é para chegar neste ponto onde quero declarar explicitamente minha nova “paixão” (deixando claro para minha doce Claudia, “paixão profissional!”). Depois de muito adiar, aproveitando essa pandemia, dediquei parte do meu tempo a estudar os bancos de dados orientados a grafos na desconfiança de que eles seriam uma abordagem interessante para lidar com esta complexidade de relações da biodiversidade, em suas diferentes camadas. Cada vez mais, me convenço disto.
Há alguns anos eu havia me interessado pelas visualizações de redes e comecei a “brincar” com o Gephi. Avancei em alguns projetos, mas o único que acabou publicado foi este aqui, do qual muito me orgulho, pois foi citado pela CBD como exemplo de análise a ser seguido por outros países. Porém, em algumas visualizações / análises percebi que o Gephi estava me limitando na sua capacidade de processar volumes consideráveis de nós e relações. Foi aí que os bancos de dados orientados a grafos ganharam minha atenção. Especialmente o Neo4j.
Esta postagem já está ficando longa. Vou tentar ir direto ao ponto, de modo bem didático:
- Bancos de Dados Orientados a Grafos, doravante chamados aqui de “BDOG”, são sistemas gerenciadores de bancos de dados que armazenam dados em estruturas de grafos – nós e relações – ao invés de documentos ou tabelas;
- “Grafo” é uma abstração matemática, baseada na teoria dos grafos, cuja estrutura é representada por “nós” (vértices) e a relação entre eles (aresta);
- Tanto nós quanto as arestas possuem propriedades, e arestas possuem uma direção.

BDOGs são utilizados quando as relações são mais importantes do que as entidades. Ele é ótimo para análises exploratórias na identificação de padrões baseados em relações complexas:
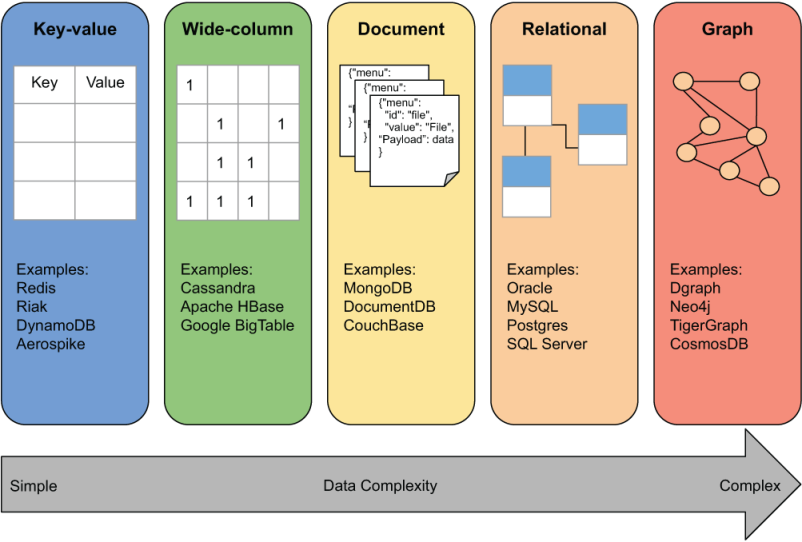
Fonte: Bechberger, D., & Perryman, J. (2020). Graph Databases in Action. Manning Publications.
É importante perceber que a popularidade dos BDOGs tem crescido bastante, inflamada pelas redes sociais, navegação e compras na Internet:
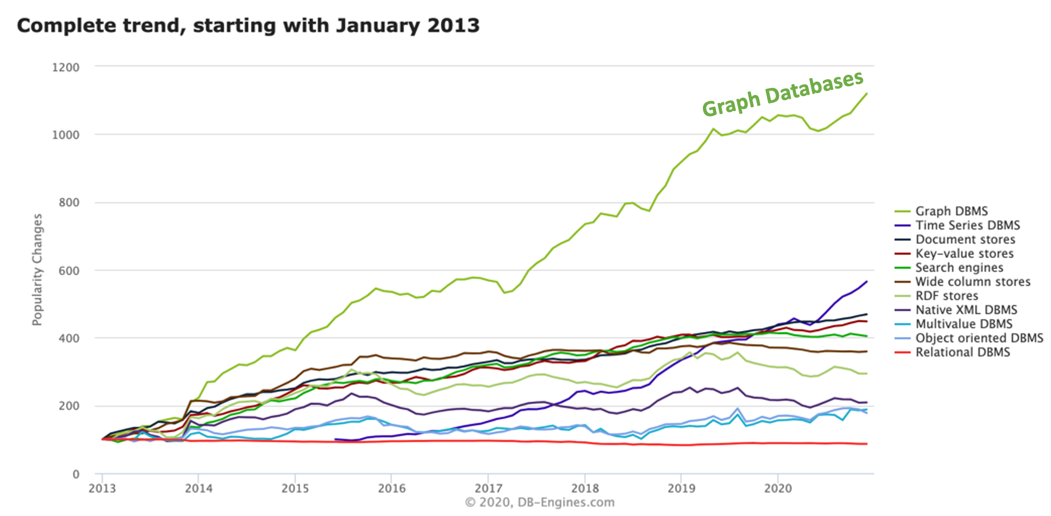
Por conta disto, com muito material e ferramentas disponíveis, podemos nos aproveitar desta nova tecnologia e explorar suas aplicações na gestão e análise de dados sobre biodiversidade.
Ando implementando alguns bancos de dados orientados a grafos no Neo4j, com base em alguns conjuntos de dados que já tinha estruturado em bancos relacionais, por exemplo, para visualizar a “transmissão do conhecimento taxonômico” através da relação de orientação na pós-graduação de participantes da Flora e Funga do Brasil, assim como a competência destes taxonomistas em relação ao taxa:
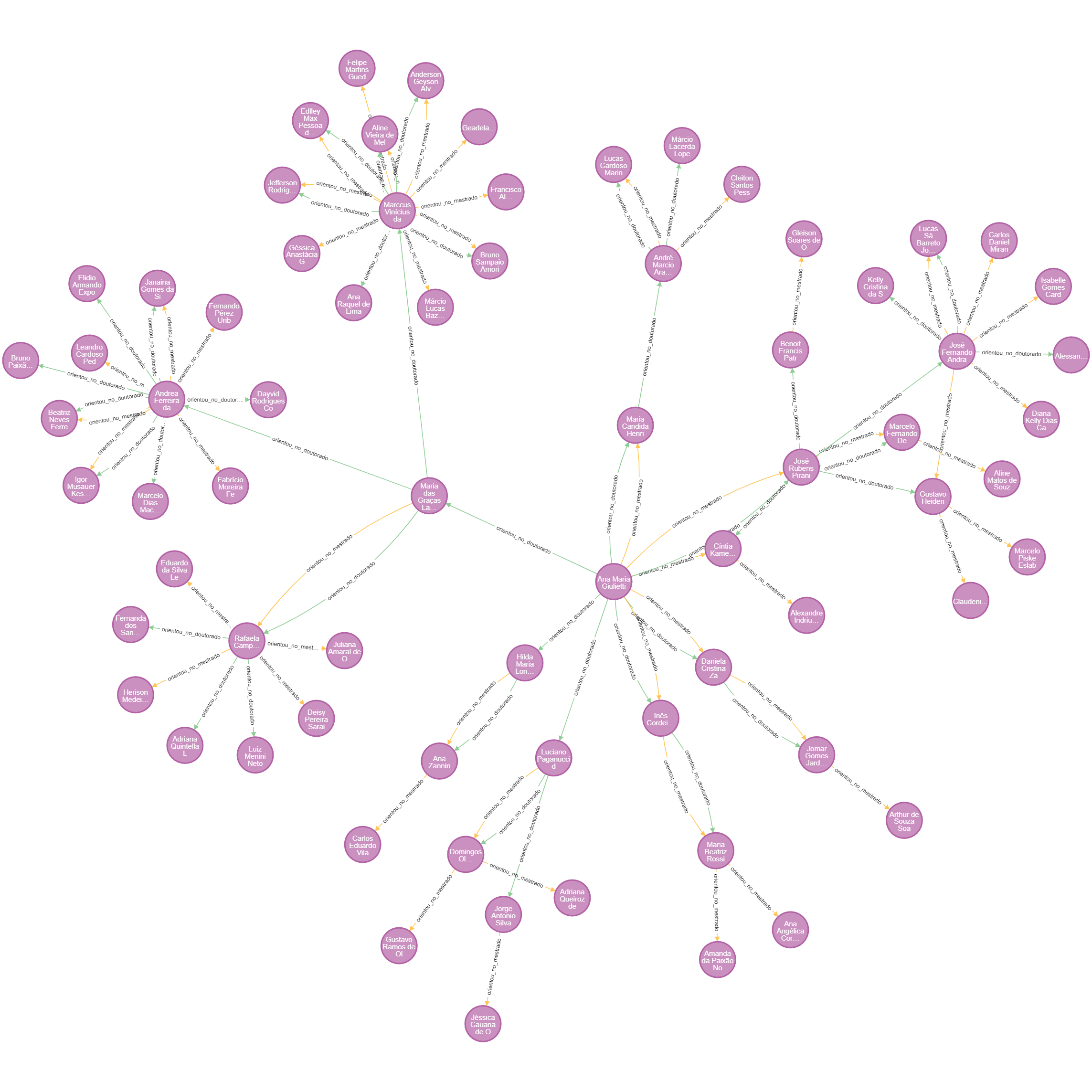
clique para ampliar
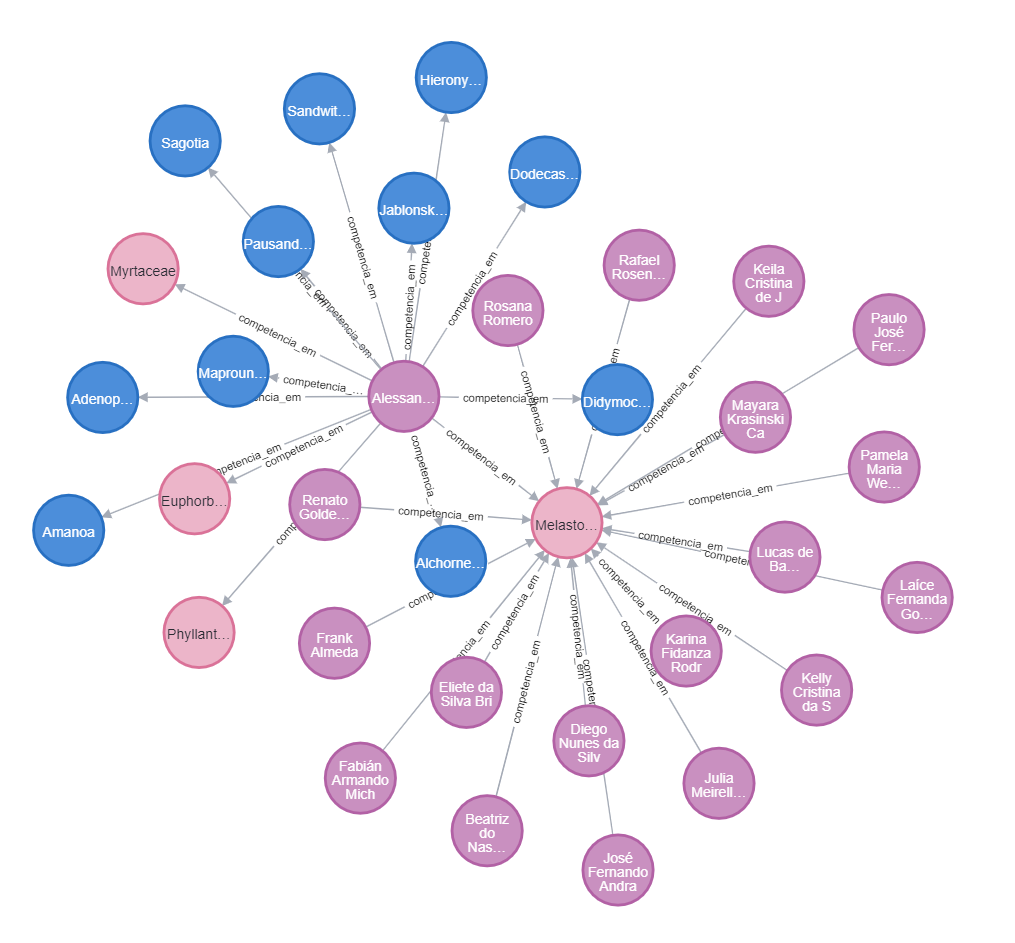
São apenas dois estudos de caso que tenho usado para desenvolver minha competência na ferramenta. Neste processo, aprendendo CypherQL, uma nova linguagem para manipular dados no Neo4j.
Após cerca de 30 anos “pensando de forma relacional”, minha cabeça ainda está re-sintonizando a visão do mundo da biodiversidade sob a forma de grafos. Mas ando me divertindo bastante riscando papel e quadro (ou usando o “arrows“), exercitando esta nova forma de modelar dados sob a forma de grafos! Fico pensando em um “supermodelo” que represente a relação das entidades biológicas com todas as outras entidades dos diferentes eixos temáticos, nas diferentes camadas. Tem tirado meu sono…
De volta ao início desta postagem, onde falamos da percepção da transversalidade da biodiversidade, gostamos de falar que “a biodiversidade tem relação com tudo”. Em minha opinião, essa pode ser a ferramenta, com bases matemáticas sólidas, onde podemos, finalmente e de forma irrefutável, provar essa afirmação!


Uma resposta para “Discutindo a relação”